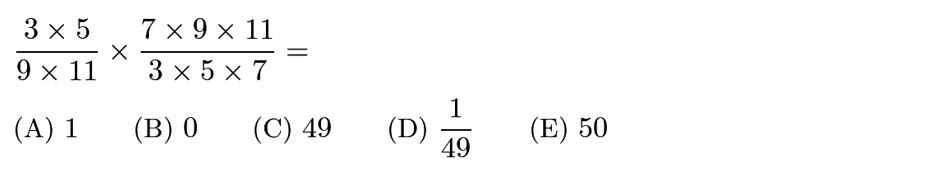
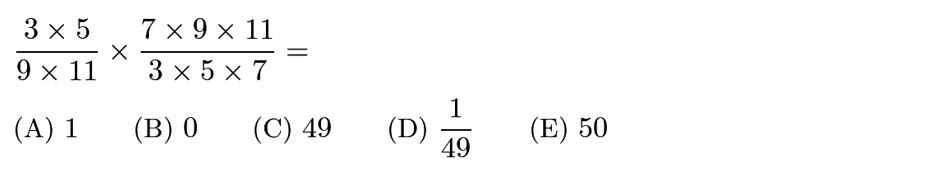
Answer: A
Solution:
(3*5*7*9*11)/(9*11*3*5*7)=1.
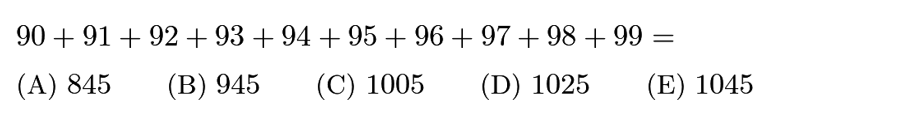
Answer: B
Solution:
We can use the formula for finite arithmetic sequences.
It is (a1+an)*n/2 where n is the number of terms in the sequence, a1 is the first term and an is the last term.
Applying it here: (90+99)*10/2=945.

Answer: D
Solution:
=10^3/5=1000/5=200.

Answer: C
Solution:
Let FG perpendicular BC at G.
ED=BC-AF=9-5=4;
ABCDEF=ABFG+EGCD=5*6+4*4=30+16=46.
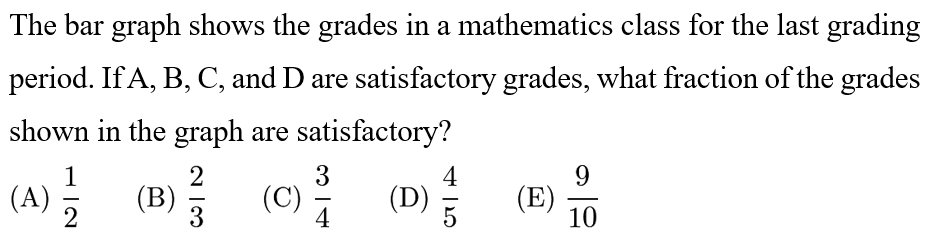
Answer: C
Solution:
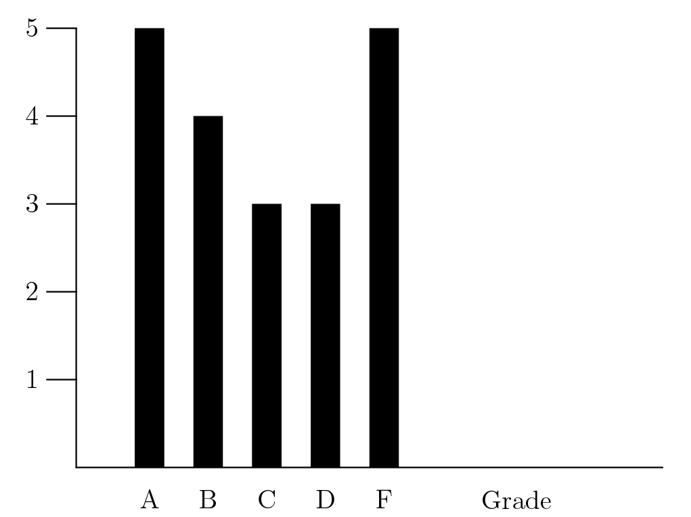
A: 5; B: 4; C: 3; D: 3; F:5;
(5+4+3+3)/(5+4+3+3+5)=15/20=3/4.

Answer: D
Solution:
500/5=x/7.5, thus x=750
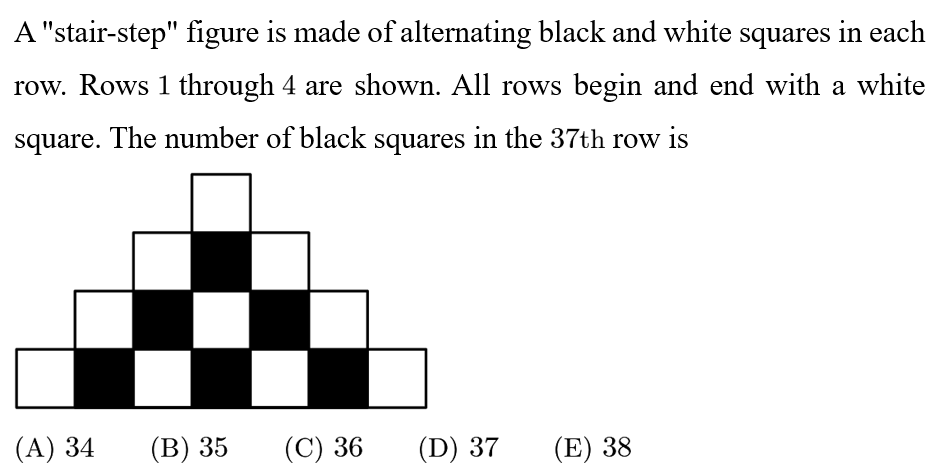
Answer: C
Solution:
The number of black squares in each rows are:
0, 1, 2, 3, ….. , so ,the 37th row is 36.
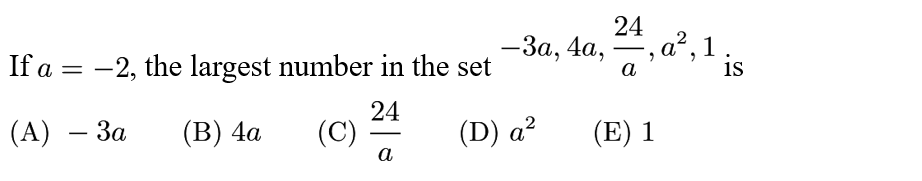
Answer: A
Solution:
we can just evaluate the set to be { 6, -8, -12, 4, 1;}
The largest number is 6, which corresponds to -3a.
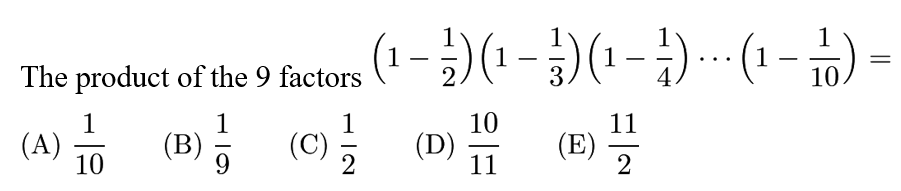
Answer: A
Solution:
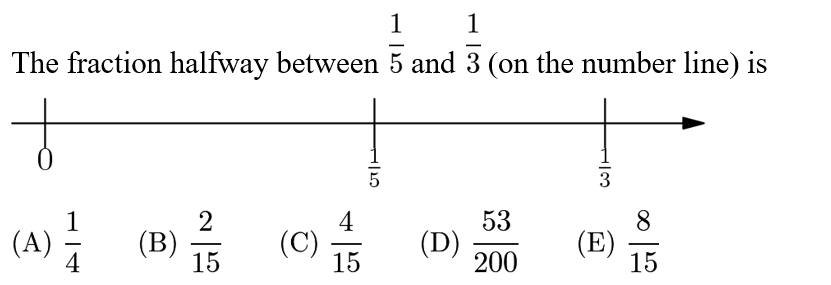
Answer: C
Solution:
The fraction halfway between 1/5 and 1/3 is simply their average, which is
(1/5+1/3)/2=4/15.

Answer: E
Solution:
To find the face opposite x, we can find the faces sharing an edge with x, so the only face remaining will be the opposite face.
The only face x doesn't share an edge with is y, which is choice E.

Answer: B
Solution:
The perimeter of the triangle is: 6.2+8.3+9.5=24. The perimeter of the square is 24 too. The length of the square is 6. Thus the area of the square is 6*6=36.
We are given the three side lengths of the triangle, so we can compute the perimeter of the triangle to be 6.2+8.3+9.5=24. The square has the same perimeter as the triangle, so its side length is 24/4=6. Finally, the area of the square is 6*6=36.

Answer: B
Solution:
45 minutes is 3/4 of an hour, so the walking contributes 3/4*4=3 miles. Similarly, 30 minutes is 1/2 of an hour, so the running adds 1/2 * 10=5 miles. Their total is 3+5=8 miles.
Answer: B
Solution:
(6.5%-6%)*20=0.1

Answer: C
Solution:
How many numbers are there that DON'T have a 2 between 100 and 400? Well, we have 2 possibilities for the hundreds digit (1, 3, note that 2 is not allowed), 9 possibilities for the tens digit (1, 3, 4, 5, ... , 9, 0), and 9 possibilities for the ones digit. 2*9*9=162. However, one of the numbers we counted is 100, which isn't between 100 and 400, so there are 162-1=161 numbers without a 2. There are 299 numbers between 100 and 400 and 161 that DON'T have any 2's, 299-161=138 numbers WILL have at least one two.
Method 2: if the hundreds digit is 2, 10 possibilities for the tens digit (1, 2, 3, 4, 5, ... , 9, 0), and 10 possibilities for the ones digit. 1*10*10=100;
if the tens digit is 2, there are 2 possibilities for the hundreds digit (1, 3), and 10 possibilities for the ones digit (1,2,3,4,…9,0). 2*1*10=20;
if the ones digit is 2, there are 2 possibilities for the hundreds digit (1, 3), and 9 possibilities for the tens digit(1,3,4,…9,0). 2*9*1=18;
totally: 100+20+18=138.

Answer: D
Solution:
Let the number of boys be 2x. It follows that the number of girls is 3x. These two values add up to 30 students, so 2x+3x=5x=50 =>x=6.
The difference between the number of girls and the number of boys is 3x-2x=x, which is 6.

Answer: D
Solution:
If the average score of the first six is 84, then the sum of those six scores is 6*84=504. The average score of the first seven is 85, so the sum of the seven is 7*85=595. Taking the difference leaves us with just the seventh score, which is 595-504=91.
Answer: E
Solution:
Let p be the cost of the first pamphlet, in dollars. The first part tells us 9p<10=>p<1.111;
The second part tells us that 10p>11 => p>1.1 . Combining these two parts, the only possible value for P is 1.11.
Answer: B
Solution:
Let the width be w and the length be l. Then, the original perimeter is 2*(w+l).
After the increase, the new width and new length are 1.1w and 1.1l, so the new perimeter is 2*(1.1w+1.1l)=1.1*2*(w+1). Therefore, the percent change is 10%.
Answer: C
Solution:
January has four full weeks and then three extra consecutive days. Each full week contributes one Tuesday and one Saturday, so the three extra days do not contain a Tuesday and Saturday. Therefore, those three days are Wednesday, Thursday, and Friday.
Wednesday is the 29th day of January, therefore the 22nd, 15th, 8th, and 1st of January are all Wednesdays, so the answer is Wednesday.
Answer: E
Solution:
Assume his salary is 100 dollars. Then in the next year, he would have 110 dollars, and in the next he would have 121 dollars. The next year he would have 133.1 dollars and in the final year, he would have 146.41. As the total increase is greater than 45%.

Answer: B
Solution:
An equivalent problem is finding the probability that a randomly selected telephone number begins with 9 and ends with 0.
There are 10-8 possibilities for the first digit in total, and only 1 that works, so the probability the number begins with 9 is 1/8.
There are 10 possibilities for the last digit, and only 1 that works , so the probability the number ends with 0 is 1/10.
Since these are independent events,the probability both happens is 1/8*1/10=1/80.
Method 2:
The total possible telephone number is : 8*10*10*10*10*10*10;
The number of telephone numbers begin with 9 and end with 0: 1*10*10*10*10*10*1
The fraction: (1*10*10*10*10*10*1)/8*10*10*10*10*10*10 =1/80.

Answer: E
Solution:
If each student has 5 classes, and there are 1200 students, then they have a total of 5*1200=6000 classes among them.
Each class has 30 students, so there must be 6000/30=200 classes. Each class has 1 teachers, so the teachers have a total of 200 classes among them. Each teacher teaches 4 classes, so if there are 200/4=50 teachers.

Answer: A
Solution:
Let the number in the top circle be a and then b, c, d, e, and f, going in clockwise order. Then, we have s=a+b+c, s=c+d+e, s=e+f+a.
Adding these equations together, we get 3s=(a+b+c+d+e+f)+(a+c+e)=75+(a+c+e).
The largest possible value of a+c+e is 15+14+13=4, and the corresponding value of s is (75+42)/3=39.

Answer: A
Solution:
Logically, Jane's statement is equivalent to its contrapositive, ”If an even number is not on one side of any card, then a vowel is not on the other side.”
For Mary to show Jane wrong, she must find a card with an odd number on one side, and a vowel on the other side. The only card that could possibly have this property is the card with 3.
AMC培训、答疑,请联系微信 / 电话:136 1118 1627
艾蕾特教育 @Elite Edu, 在这里,